はじめに

ラグランジュの不変量（Lagrange’s Invariant）は結像を考える上で最も大事な式の一つです
物体側の「高さ・開口角・屈折率」と像側の「高さ・開口角・屈折率」の関係を示します

また、ビーム伝搬、光ファイバーへのエネルギー導入光学系、液浸レンズの使い勝手等を考える上で重要です

ラグランジュの不変量を考える

※　ここでは前後の屈折率が同じとして考えます
※　ラグランジュの不変量は近軸式 ・・・ u ≒ tan(u) ≒ sin(u)

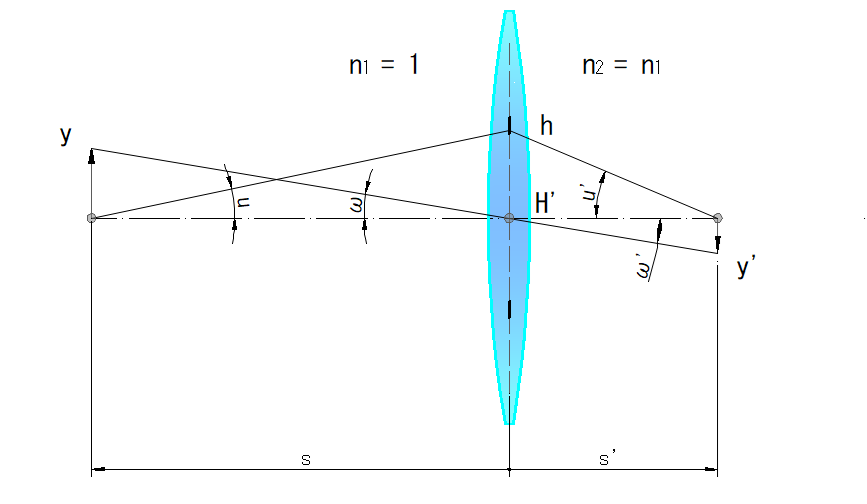
下記図において、　
u = h / s, u’ = h / s’
h = u / s = u’ / s’
u / u’ = s / s’ ・・・ ①

ω = ω’ = y / s = y’ / s’
y / y’ = s / s’ ・・・ ②

①、②式より
uy = u’y’ ・・・ ③

例１）ビーム伝搬とラグランジュの不変量

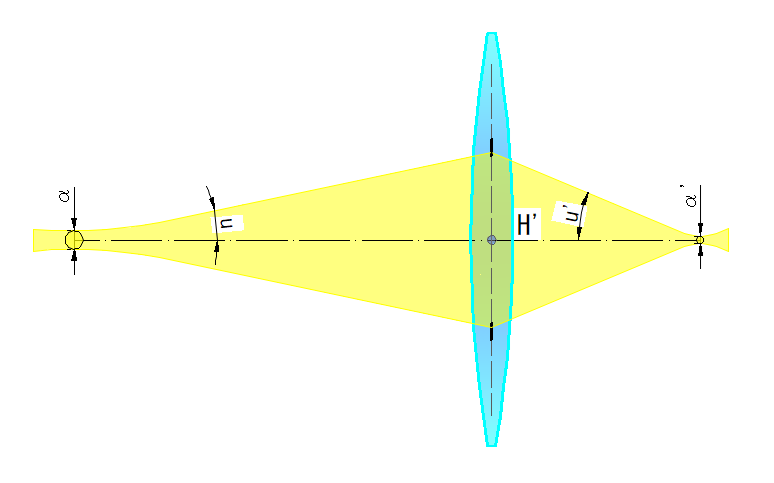
ビーム伝搬はラグランジュの不変量に相似した考え方が成り立ちます
下図において、入射角 u のビーム直径 α に対し、射出角 u’ の場合、下記式が成り立ちます

uα = u’α’

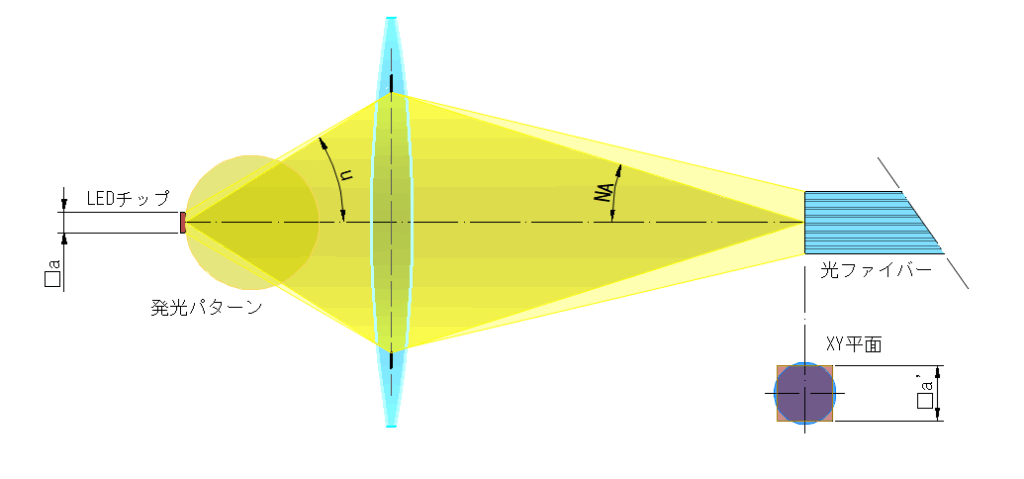
例２）光ファイバー エネルギー導入光学系とラグランジュの不変量

光ファイバーは情報伝達、エネルギー伝搬において重要です

下図は照明光学系におけるLEDチップから光ファイバーへの導入光学系の概要です
LEDの発光パターンはほぼランバート発光で、チップは面積があり倍率の考慮が必要です
光ファイバーは導光可能なNAと入射径の制約があります

最適化はまず倍率の仮決定で、光ファイバーの入射面にLEDチップの像を合わせます
次に入射側のNAをラグランジュの不変量の式を用いて算出します

概略の光学系を検討後、最終的に照明解析により最適倍率などの調整を行います