はじめに

媒質界面での光の屈折はスネルの法則として定義され、射出角は、媒質の屈折率と入射角の正弦値として求まる値です
光学の主仕様の開口数（NA)や角倍率、主式のラグランジュの不変量や正弦条件等、多くの諸仕様や式は三角関数を用いて算出されます
また光は横波で正弦波、干渉や偏光を考える上で時間軸上での正弦波の理解が必要です

このようなことで「三角関数を簡便に理解するには」をテーマに、

三角関数

❍　三角関数の関係式の理解

三角関数は英語表記で ‘Trigonometric Function​s’ あるいは ‘Circular Functions’
‘Circular Functions’ と表記されることからも分かるように三角関数は「円関数」です
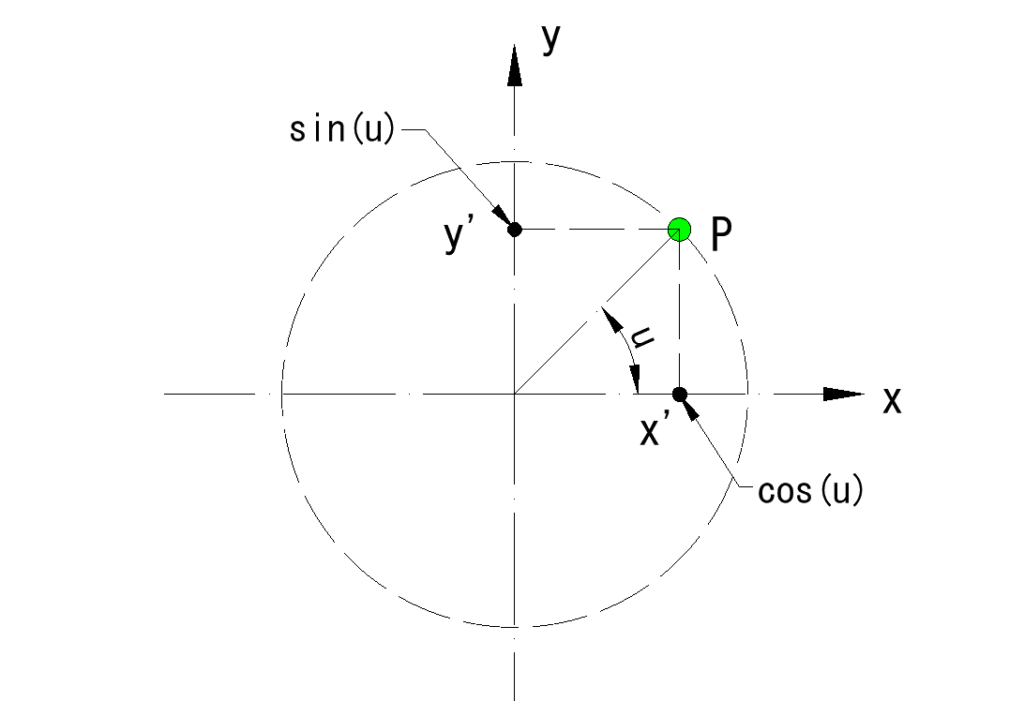
下図のようにXY平面上の原点を中心とする半径 [1] の円を考えます
点PのX軸と織りなす角度を [u] とすると、正弦 sin(u)の値はY軸上の y_p の値、余弦 cos(u)の値はX軸上の x_pの値

下図より、
sin(u)はcos(u)より90°（π/2 rad）遅れた、あるいは cos(u)はsin(u)より π/2 rad 進んだ状態と考えられるので
sin(u )= cos(u – π/2) ／ cos(u) = sin(u + π/2)

X_pの２乗とy_pの２乗の和は半径の２乗なので
sin(u)² + cos(u)² = 1²
sin(u) = √(1 – cos(u)²) ／ cos(u) = √(1 – sin(u)²)

tan(u) は y_p/x_p なので、
tan(u) = sin(u) / cos(u) ／ sin(u) = tan(u) ・ cos(u)

等々、図を思い描くと様々な式が導きだせます

※　上述のようにXの値が cos （余弦） 、Yの値が sin （正弦）、Xの値に対するYの値が tan （正接）と考えると理解しやすいと思います

❍　時間軸を考慮した正弦式

光は横波で、電場・磁場の動きは時間軸上での正弦波として表されます
また干渉や偏光は電場の波どうしの重ね合わせで理解されます

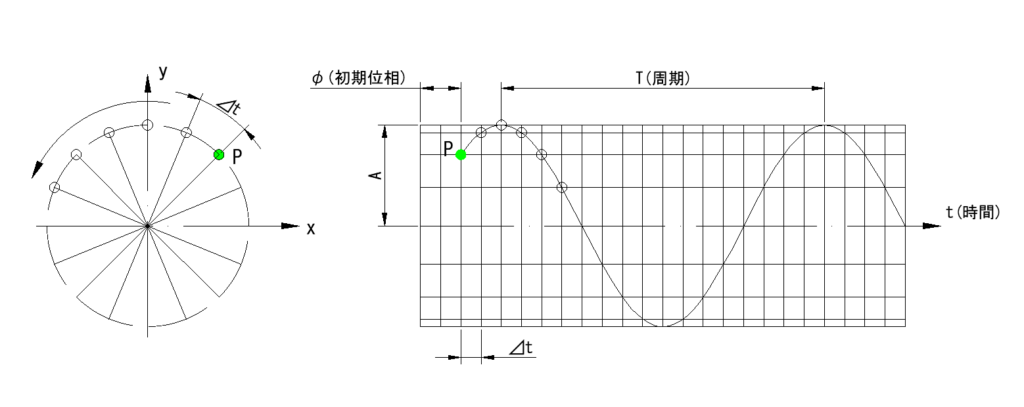
正弦波は左図の円周上を等角速度で移動する点の振幅（ｙ）を縦軸に、時間軸を横軸に取ってプロットした波です

正弦波の時間との関係式は、

※　角周波数ωは点Pが円周上を単位時間当たりどの程度移動（回転）するかを示す値
　　周期との関係は
　　ω = 2π / T（周期）

❍　弧度（radian）

三角関数で使用する角度は弧度です（単位は rad ）
弧度は円弧の長さを角度の値としたものです

※　円周率πは直径に対する円周全長との比
　　半径１の全円周長は２πで、半円周長はπ（180°）

❍　三角関数の略式

角度 u が小さい場合、sin(u)の値とその円弧の長さは同じと考えられるため、

　sin(u) ≒ tan(u) ≒ u
　cos(u) ≒ 0

と近似する場合があります（光学の近軸式はこの考え方です）