はじめに

光の速度は媒質によって変化します
例えば、真空中の光の速度は約30万km/ sec.ですが、水中では約22.5万km/ sec.

真空中での光の速度と媒質中での光の速度の関係（逆数）が屈折率です
以下、光の速度と屈折率の関係について

光の速度と屈折の関係

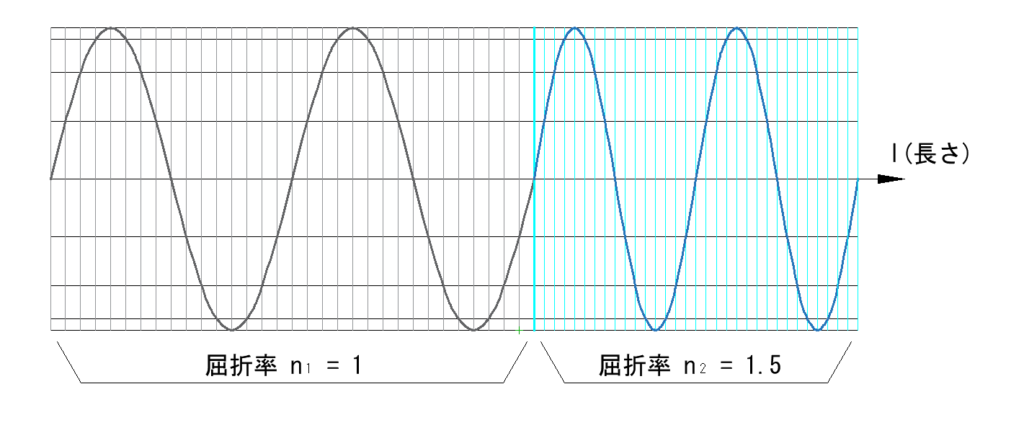
下左図は横軸が長さ、縦軸が振幅
光（正弦波）が屈折率（n₁ = 1）の媒質から屈折率（n₂ = 1.5）の媒質へ進む様子
光の絶対量は周波数（周期）で、これに対し速度と波長は媒質によって変化します
真空中の光の速度に対し、ある媒質を進む光の速度との比がその媒質の屈折率です

※　光の速度の基準を真空とした媒質の屈折率を絶対屈折率、
　　　大気の屈折率を基準とした値を、相対屈折率あるいは単に「屈折率」と称します
　　人工衛星のカメラなど真空中で使用する機器はまれなので、光学設計では大気を基準とした（相対）屈折率を用います

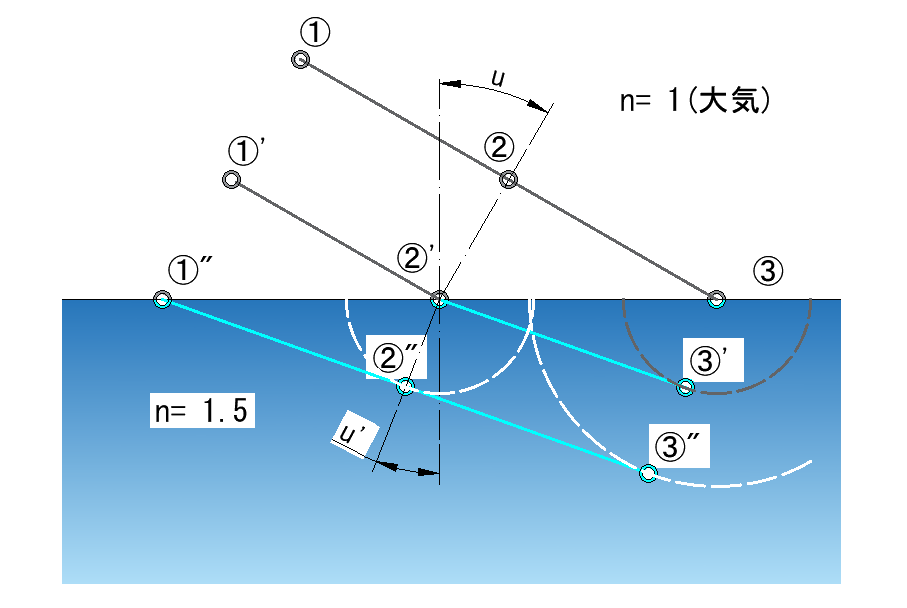
光の速度と媒質界面での屈折の関係を示したのが下右図
大気（n₁ = 1）から屈折率（n₂ = 1.5）の媒質へ、平面波が入射角 u で入射した状態

平面波「①-②-③」の③が媒質界面に到達し、等時間経過後「①’-②’-③’」→「①”-②”-③”」と進行する様子
「①”-②”-③”」において②”は、②’を原点とする円弧（白の点線）上に、③”も同様に円弧（白の点線）上に進みます
同一媒質内では波面は保持されるので①”と②”、③”の接線が媒質内での平面波になります

媒質界面での光の進行方向の変化（偏向） は光の速度と密接な関係があります
また、下左図のように波長の変化と考えることもできます
基準とする媒質内の光の速度とある媒質での光の速度の逆数が屈折率です

※　光学的に「ヘンコウ」には２通りの意味・・・「偏光」　「偏向」
　　発音は同じですが、意味は異質です

屈折の式（入射角と射出角の関係）

❍　はじめに

上右図において、入射角度 u が小さい場合の入射角 u と射出角 u’ との関係は

nu ≒ n’u’・・・①

ただし、①式は入射角が大きくなるに従い誤差が大きくなります

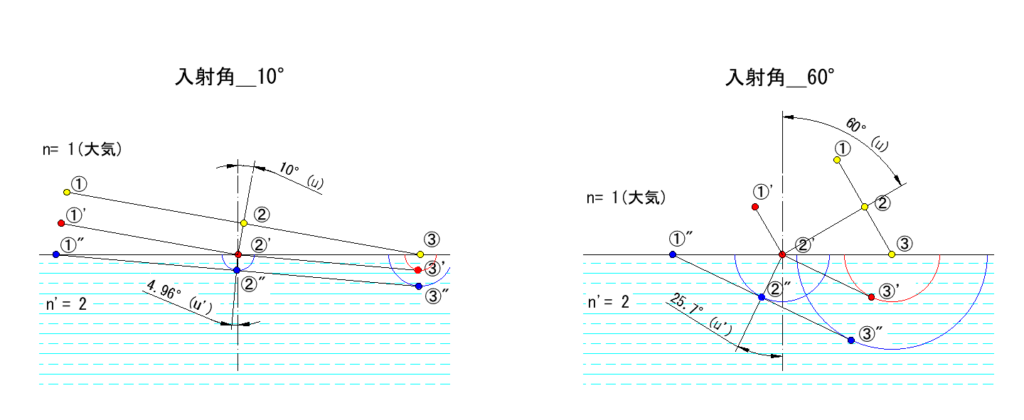
下図はCADで正確に作図したもので、大気から屈折率（n’ = 2）の媒質に入射角10°と60°で入射した状態です
入射角10°の場合は媒質界面での射出角は4.96°と上記①式とあまり差異（0.6％）がありませんが、
入射角60°の場合は射出角は25.7°と差異（14.3％）が大きくなります

❍　屈折の式（スネルの法則）

媒質界面での屈折の式を正確に導き出したのがヴィレブロルト・スネル（Willebrord Snell ）です
その屈折の式は、

n sin(u) = n’ sin(u’)・・・②

上記「光の速度と屈折の関係」のように屈折率は光の速度の逆数なので
真空の光の速度を v 、媒質内の光の速度を v’ とすると

v / v’ = n’ / n = sin(u) / sin(u’)・・・③

※　屈折の式はスネルによる実験式ですが、マックスウェルお電磁方程式を用いて算出できます

❍　正弦関数の級数次数と光学との関係

正弦関数を級数展開すると、

sin(u) = u – 3! u³ + 5! u⁵ – 7! u⁷ ・・・

光学的な意味合いとして、
　　１次の u の値・・・近軸式
　　３次の 3! u³ ・・・３次収差
　　5! u⁵ – 7! u⁷ ・・・高次収差