スギナHD株式会社

光学設計・映像編集・機構設計

１３）解像力＿MTF

光学設計上、解像力の指標となるのがMTFです
以下、MTFについて、また様々なMTF表記方法について

MTF (Modulated Transfer Function) は空間周波数、空間伝達関数、コントラスト伝達関数あるいは変調伝達関数と呼ばれます
MTFはオーディオなどの周波数特性と同じで、入力に対する出力比です
ただオーディオの周波数特性と下記の相違点があります

・増幅ではなく減衰のみ
・回折の影響があり周波数に対し限界値（回折限界）がある

基本の入力値は正弦波で、その概要を下図に示します
　　下右図＿正弦波のコントラストを持つチャートを物体側に配置したもの　
　　下右図＿レンズを通し倍率 0.5x で結像した図

※　MTFの値（Modulation）は物体側のチャートの振幅 h に対する像の振幅 h’ の比

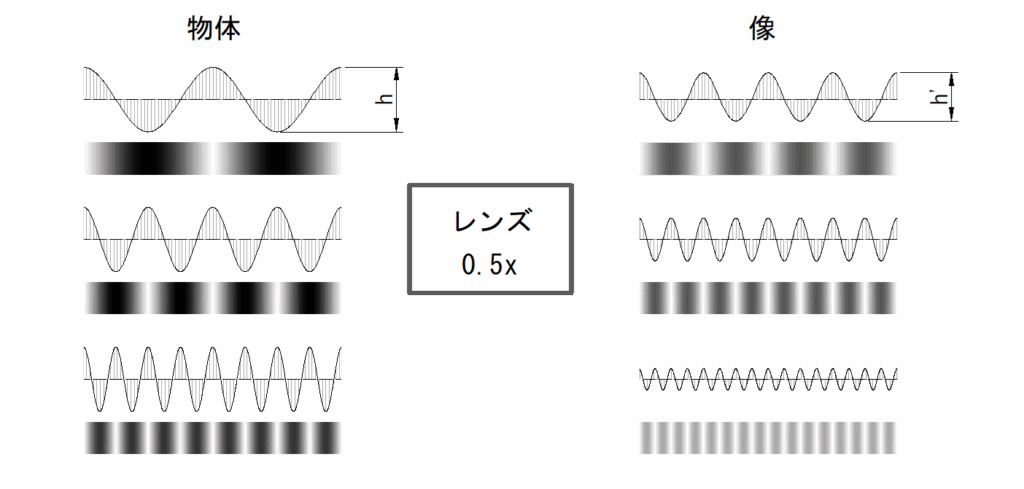
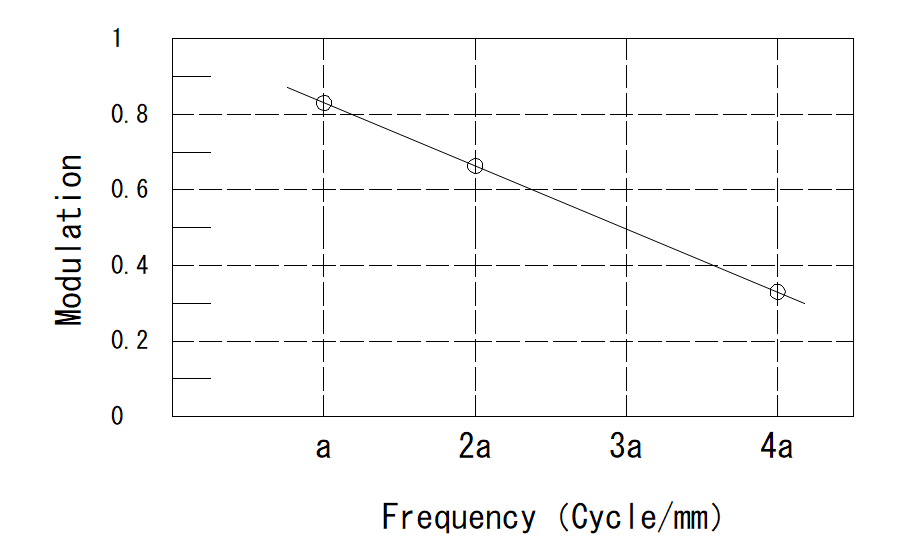
上右図の上図の周波数を a とすると、中図の周波数は 2a 、下図は 4a
この周波数を横軸に取り、縦軸を物体側のチャートの振幅 h に対する像の振幅 h’ の比を取ると下図になります
この図は解像力を表す代表的なMTTF図です

オーディオなどの電子機器の場合、入力信号を変調することは比較容易です
これに対し光学評価の場合、幾種類もの正弦波コントラストチャートを準備する必要があり効率的ではありません

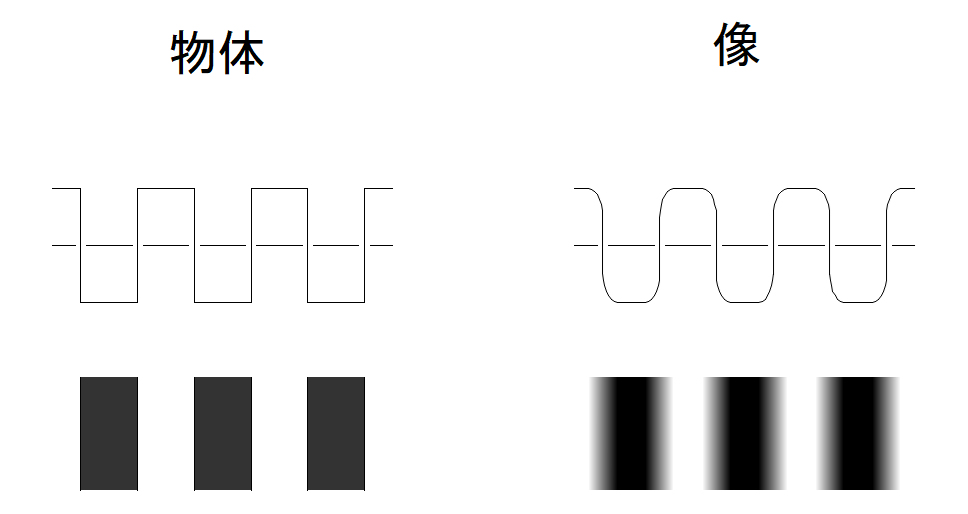
実際には、下左図の「白黒チャート」を使用します
　　下右図に倍率 1x の像のコントラストを示します

以下、白黒チャートの像情報から周波数に対するMTF値を算出する方法について

繰り返し信号は正弦波、余弦波の総和として表現できます・・・フーリエ展開
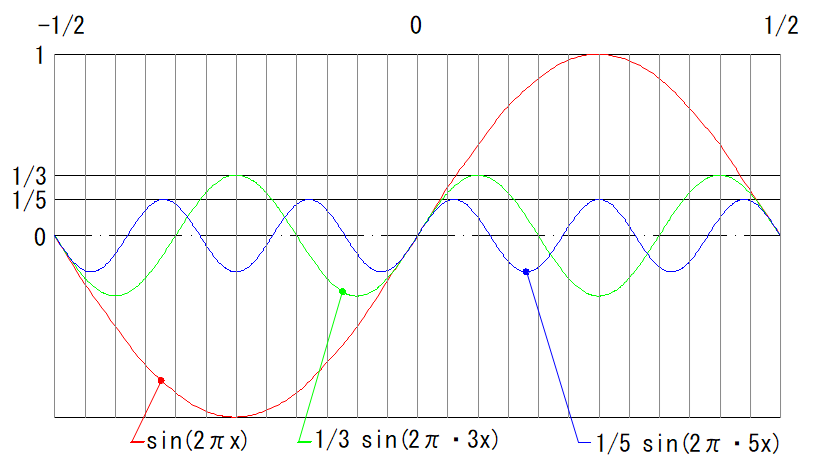
上右図の格子状波形をフーリエ展開すると

I(x) = sin(2πx) + 1/3sin(2π・3x) + 1/5sin(2π・5x) + ・・・・

この正弦波を示したのが下左図、下中図は第１項と第２項を加算、下右図はそれに第３項を加算
加算する項数を増やしていくと白く黒チャート（格子状波形）になります

また上右図の像空間のコントラストも同様にフーリエ展開（変換）することが可能で、各周波数の振幅を求めれば周波数に対するMTF値が算出できます

※　測定ではシャープエッジのコントラスト像を微分してフーリエ変換して像品質を測定します
※　設計ソフトでは、点像をフーリエ展開しMTF値を算出します

前項「MTFとは？」で示した横軸を周波数に取ったMTF図以外に、下図のようなMTF図があります

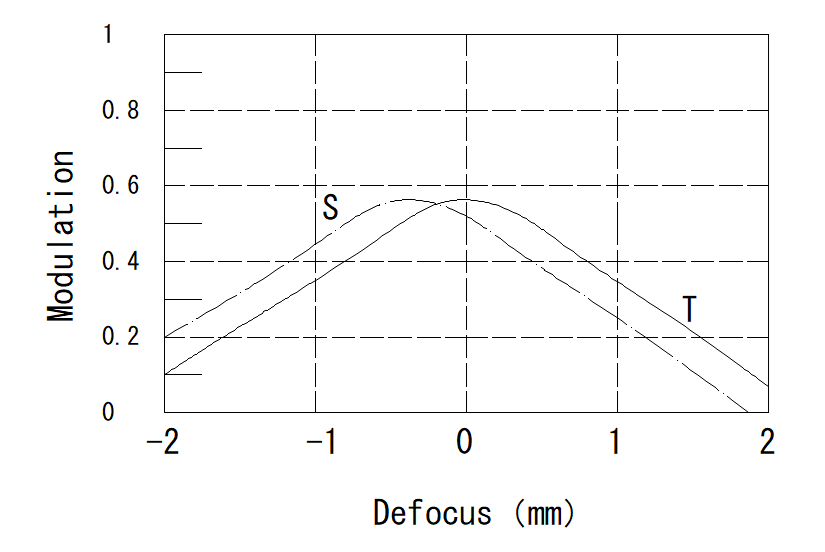
下左図はデフォーカス量を横軸に取ったもので、非点収差や像面湾曲の状態を把握したり、物体距離を変化させ被写界深度を確認するために使用します
また、波長の重みを赤 [1] 緑 [0] 青 [0]などと単色に設定し軸上色収差の評価に用います

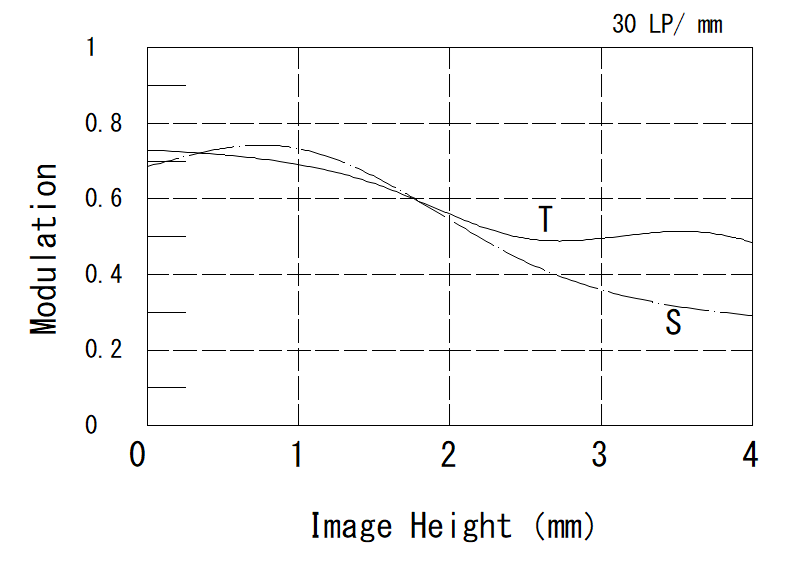
下右図は横軸に像高さを取ったもので、カメラレンズの性能評価に多く使用されます