はじめに

光学系の倍率の定義は、その光学系の用途によって様々です
カメラレンズ等の結像光学系、望遠鏡などのアフォーカルな光学系、接眼レンズなど

以下、倍率と「物体距離・レンズの焦点距離・像距離」の関係について

結像光学系の倍率

❍　ピンフォール光学系

結像光学系の倍率は物体の大きさに対する像の大きさ
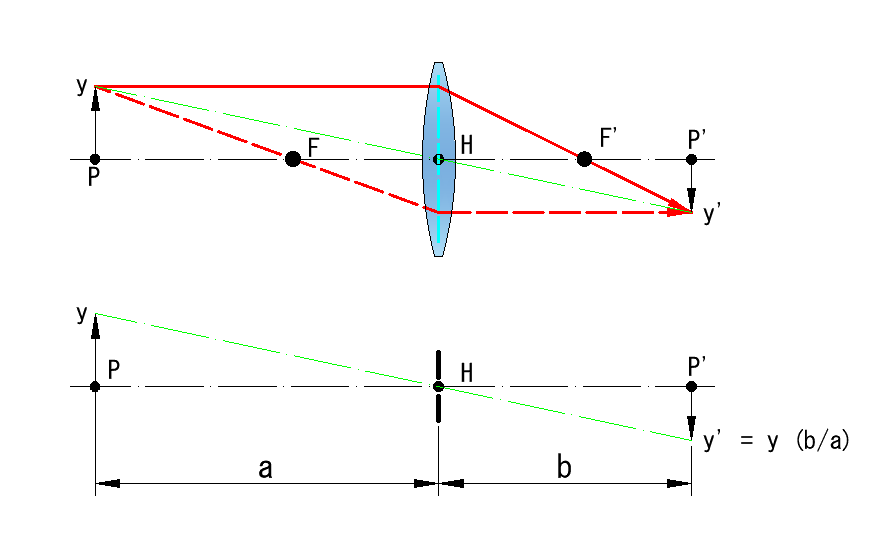
下上図は前ページの「 ４）結像の考え方」で使用した図です

　　P＿物点　　P’＿像点
　　F＿前側焦点　F’＿後ろ側焦点
　　ｙ＿物体高さ　　ｙ’＿像高さ
　　H＿薄肉レンズの主点

物体からの光軸に平行に進む光線はF’を通過し、Fを通過する光線は光軸と平行になりその接点が像位置

下図はその光線を省き、主点Hを通過する光線のみ記載した図

　　a＿物点から主点までの距離
　　B＿主点から像点までの距離

この光学系は主点位置にピンフォールを置いた状態と同様で、この倍率mは、

m = y/ y’ = y (a/b)

❍　焦点距離を基準に考えると

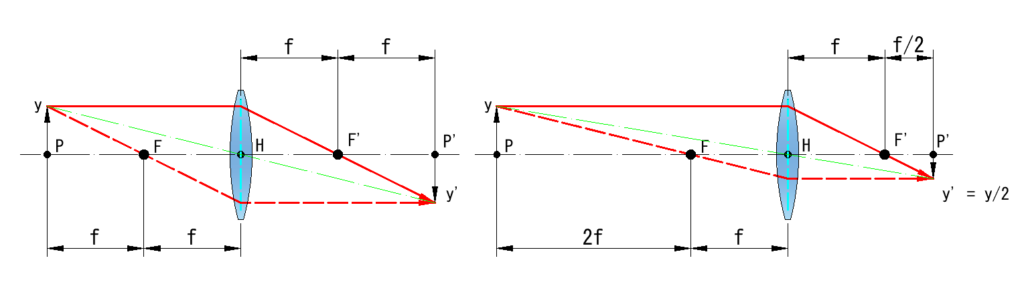
下左図は物点PとFの距離をレンズの焦点距離 f に配置した図
図からお分かりのように、像はF’から f の距離に結像し、倍率は 1x です

右図は物点PとFの距離をレンズの焦点距離 2f に配置した図
図から、像はF’から f /2 の距離、倍率は 1/2

※　 倍率は、焦点距離 f を物点から前側焦点Fまでの距離で割った値
　　像位置は、F’から f に倍率をかけた距離

※　倍率に関し、上述のピンフォール光学系に当てはめると、
　　a/b = (f + 0.5f) / (2f + f) = 0.5

アフォーカル光学系の倍率

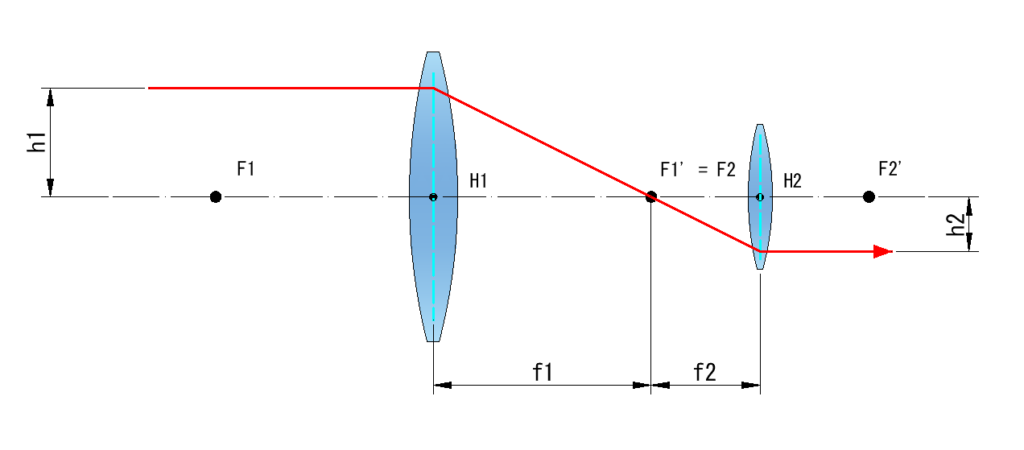
アフォーカル光学系の倍率は入射光線の光線高さと射出光線の光線高さの比で定義されます
図からも分かる通り、倍率（光線高さの比）は焦点距離の比です

m = h₂ / h₁ = f₂ / f₁・・・①

※　アフォーカル光学系は下図のように凸レンズを組み合わせるタイプと、凹レンズと凸レンズを組み合わせるタイプがあります
　　凹レンズと凸レンズを組み合わせるタイプでも上記①式は同様です

角倍率

上記アフォーカル光学系では光軸に平行な光線が入射する場合に多く使用されます
斜入射の場合には、角倍率を使用して光学系の倍率を定義する例が多いです

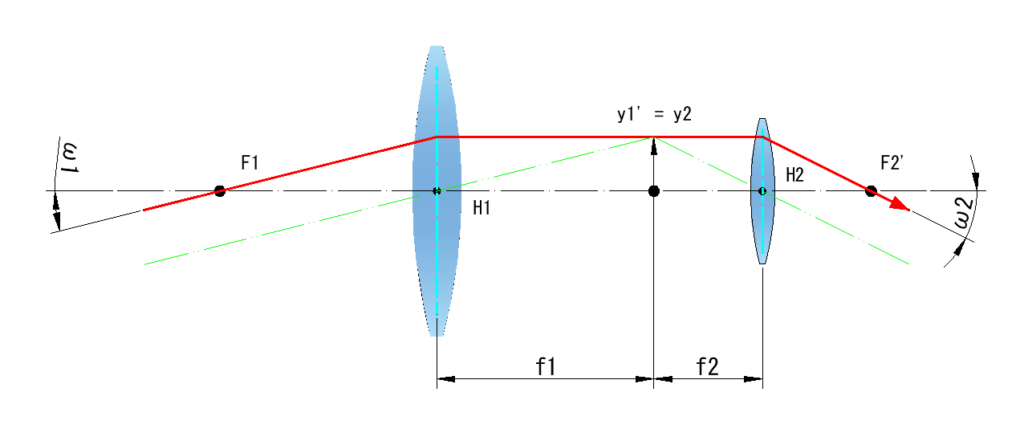
下図は前側レンズの前側焦点F_１を通過する光線（赤）と各レンズの主点を通過する光線（緑）を記載してます

　　ω_１＿入射角度　　ω_２＿射出角度
　　y_１（= y₂）＿前側レンズの像高さ

前側レンズに無限遠からω_１で入射する光線の像高さは

y_１‘ = f₁ tan(ω₁)

後側レンズの後面から入射角ω_２で入射する光線の像高さは

y₂ = f₂ tan(ω₂)
y₁‘ = y₂ 　なので

f₁ tan(ω₁) = f₂ tan(ω₂)
ここで、角倍率をm_aとすると　　
m_a = tan(ω₂) / tan(ω₁) = f₁ / f₂

接眼倍率

一般的な方が最も見やすい物体距離を明視距離と言い、その距離は 250 mmとされます
この明視距離で見える大きさを基準として、どの程度大きく見えるかを表したのが接眼倍率です

例えば、焦点距離50 mmのレンズを通して見ると、レンズの前側主点から約50 mm程度のところでよく見えます
また、上述の角倍率が約５ｘになり、５ｘ大きく見えます

このような事から、接眼倍率は明視距離をレンズの焦点距離で割った値を用います

※　眼はフォーカス調整機能（焦点距離の変化）があり、また眼とレンズ間隔によって倍率も変化します
　　また、大きく見えること自体が感覚的なもので、接眼倍率はある程度の指標です