はじめに
レンズの焦点距離を算出する公式を下記に示しますが、パッと見良く分からないかもしれません
と言うことで、以下図を用いながらレンズの焦点距離の概要について
薄肉レンズの焦点距離
1 / f = (n – 1) (1 / r1 – 1 / r2)
厚肉レンズの焦点距離
1 / f = (n -1) (1 / r1 – 1 /r2) + (d /n) ((n – 1)2 / r1r2))
f _ レンズの焦点距離
n _ レンズの屈折率
r1_ レンズ第一面の曲率半径
r2_レンズ第二面の曲率半径
d _レンズの厚み
レンズの焦点距離
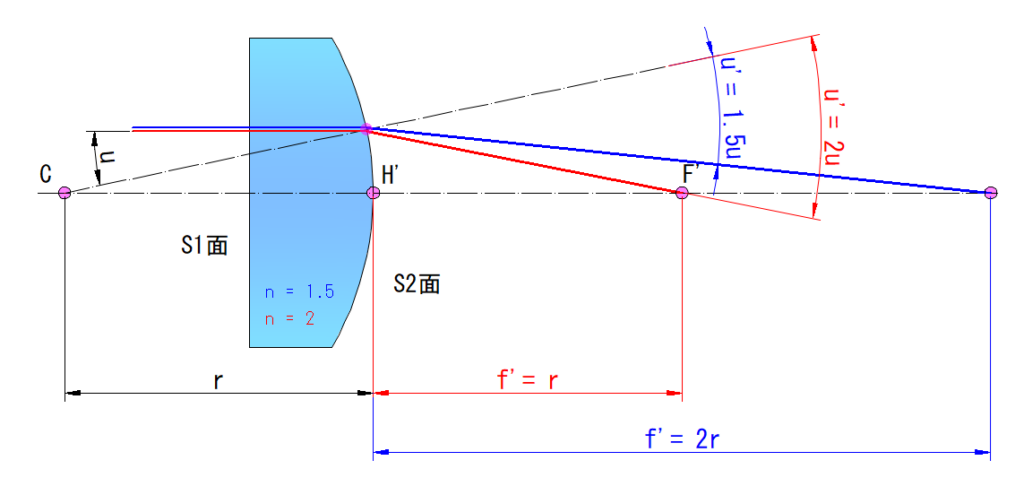
下図に平凸レンズに光軸と平行な光線が入射した様子を示します・・・屈折面は後面(S2面)のみ
赤の光線がレンズの屈折率(n = 2)、青の光線はレンズの屈折率(n = 1.5)の場合
S2面の光線入射角度 u とすると、屈折率(n = 2)レンズの射出角 u’ は 2u 、屈折率(n = 1.5)レンズは 1.5u
後側主点H’と射出光線が光軸と交わる点の距離は屈折率(n = 2)レンズ r 、屈折率(n = 1.5)レンズは 2r
この事から、レンズの焦点距離はレンズの屈折率と関係があり、大気との屈折率差に逆比例することが分かります
焦点距離はレンズの曲率半径と大気とレンズの屈折率差 ⊿n によって求まる値で
f = r/ ⊿n
※ この説明_無理があるとよく言われるのですが、レンズの屈折率を 1.333, 1.25・・・と追加して考えて頂ければ
合焦点距離
複数の面や複数のレンズの合焦点距離を算出する場合、各面あるいは各レンズの焦点距離の逆数の計算になり、少々わかりずらいです
このため、焦点距離の逆数を光学パワーφとすると理解しやすいと思います
・・・ φ = 1/ f
厚みが無視できる2枚のレンズが近接する場合、合光学パワーは単純に加算された値
・・・ φ ≒ φ1 + φ2
例えば、厚みが無視できる焦点距離 10 mmのレンズが近接する場合、その合光学パワーφは
・・・φ ≒ 1/ f1 + 1/ f2 = 0.2
従って、合焦点距離は 5 mm
2枚のレンズ間隔が伸びると合光学パワーは次第に小さくなり、間隔の影響が無視できなくなります
⊿_前側レンズの後ろ側主点位置と後側レンズの前側主点間の距離とすると、この場合、
・・・φ = φ1 + φ2 – ⊿ φ1 φ2 ・・・ ①
例えば、2枚の焦点距離 10 mmのレンズが⊿ = 5 mmの場合
φ = φ1 + φ2 – ⊿ φ1 φ2 = 0.1 + 0.1- 5・0.1・0.1 = 0.15
従って、合焦点距離は 6.67 mm
※ ①式は覚えやすく便利です
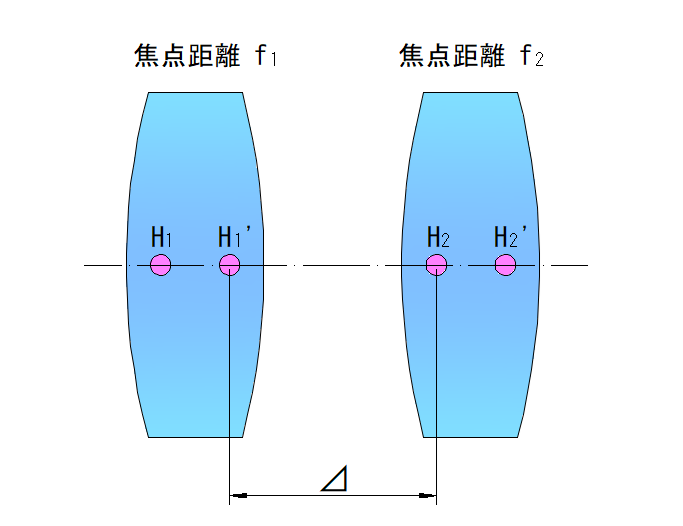
前側レンズ
f1_ 焦点距離
H1_ 前側主点
H1‘_ 後側主点
後側レンズ
F2_ 焦点距離
H2_ 前側主点
H2‘_ 後側主点
⊿_H1‘とH2の距離
ミラーの焦点距離
下図はミラーに光軸と平行な光線が入射した状態
その入射角を u とすると、射出角は u’ = u になり、光軸と交わる点(焦点 F’)は曲率半径 r の1/ 2です
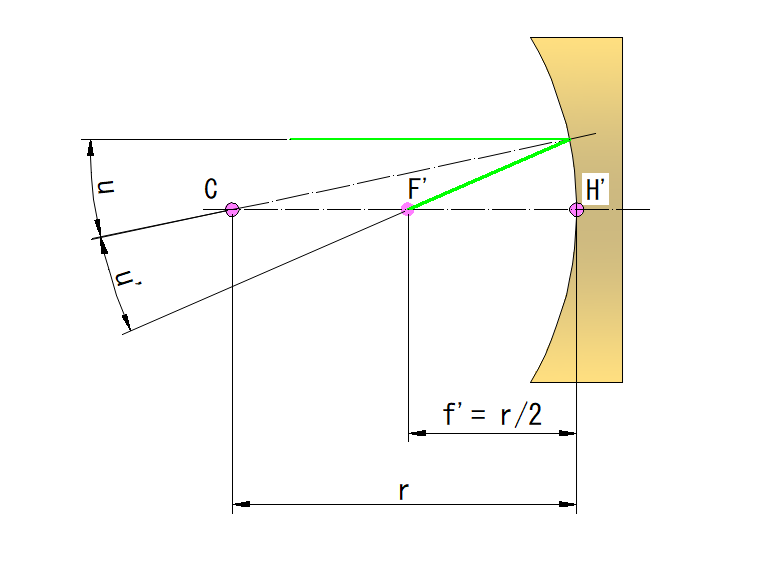
C_ ミラーの曲率中心
F’_ 焦点位置
H’_ 主点位置
U_ 入射角
U’_ 射出角
