はじめに
周辺光量比は像面照度比あるいは周辺減光とも呼ばれ、像面の中央部に対する周辺部の明るさの割合です
入射瞳にωの角度で入射する物点の像はコサイン4乗(cos(ω)4)に比例して暗くなります
以下、コサイン4乗則について
軸外物点の光量
どの方向から見ても輝度が均一な面を完全拡散面と言います
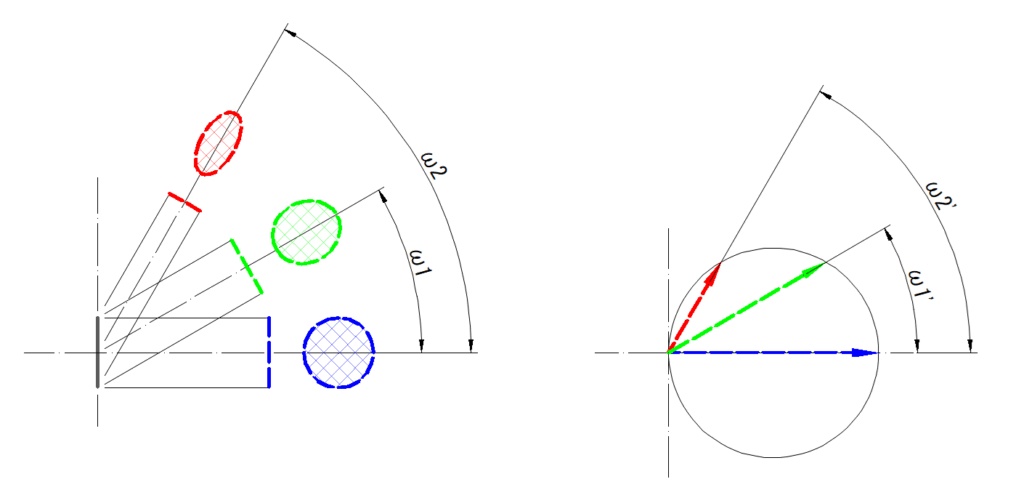
この完全拡散面において、下左図のようにある物体(灰色の実線)を観察した場合、その物体の光量は各色の網掛けで示す値です
これを書き直したのが下右図・・・明るさは観察する角度の余弦値
※ 完全拡散面の反射をランバート反射( Lambertian reflectance)と称します
物体距離の影響
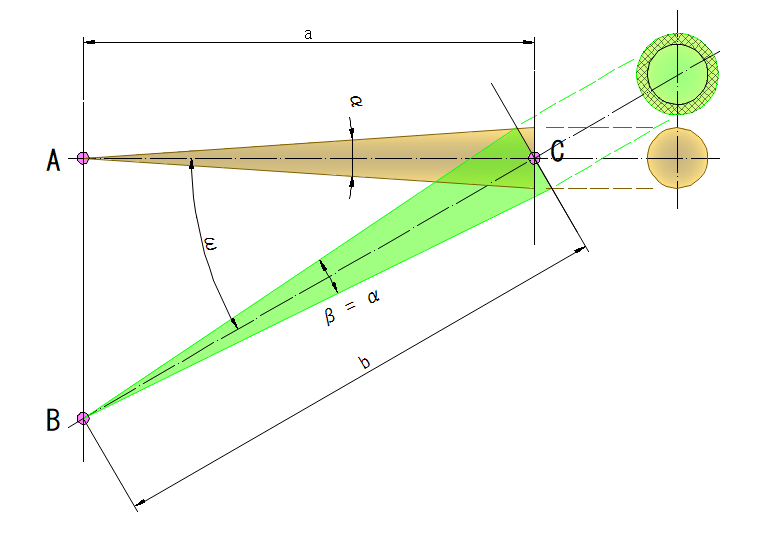
下図は光軸上の物点Aから入射瞳Cへ向かう立体角αの光線束と、軸外物点Bから入射瞳C点へ向かう立体角β(= α)の光束を示します
物点Aから物点Cまでの距離 a に対し物点Bから物点Cまでの距離 b は
b = a/ cos(ω)
従って、物点Bからの入射瞳位置での光束径も同様に a/ cos(ω)だけ大きくなります
明るさは光束の断面積比で、軸外物点の明るさは入射瞳への入射角ωのコサイン2乗で暗くなります
口径蝕の影響
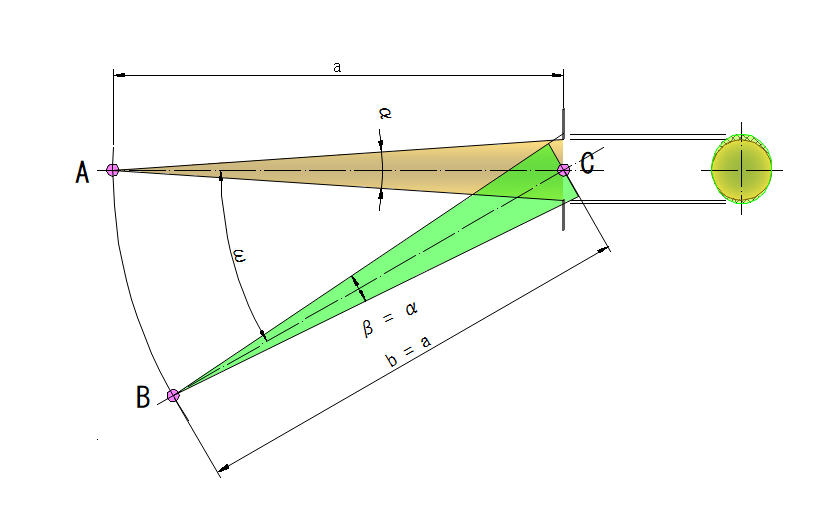
下図は光軸上の物点Aから入射瞳Cへ向かう立体角αの光線束と、立体角βと入射瞳Cまでの距離 b が同じ軸外物点Bからの光線束を示します
軸外物点Bの光線束は入射瞳上で楕円になり、入射瞳でケラレが発生します・・・口径蝕
この口径蝕により軸外物点の明るさは cos(ω)になります
コサイン4乗則
以上のように画像の周辺光量は、軸外物点の明るさ(余弦値)、物体距離の影響(余弦値の2乗)、口径蝕の影響(余弦値)により、コサイン4乗で暗くなり、これをコサイン4乗則と称します
