はじめに
正弦条件(Sine Condition)は結像レンズの必須な条件式で、コマ収差に関するものです
コマ収差は軸外物点の近軸倍率に対し、開口高さ持った光線の倍率の誤差と考えることができます
前頁のラグランジュの不変量は近軸領域での結像に関するものでした
これに対し、正弦条件は開口高さを持つ光線の像倍率に関する条件式です
正弦条件とは
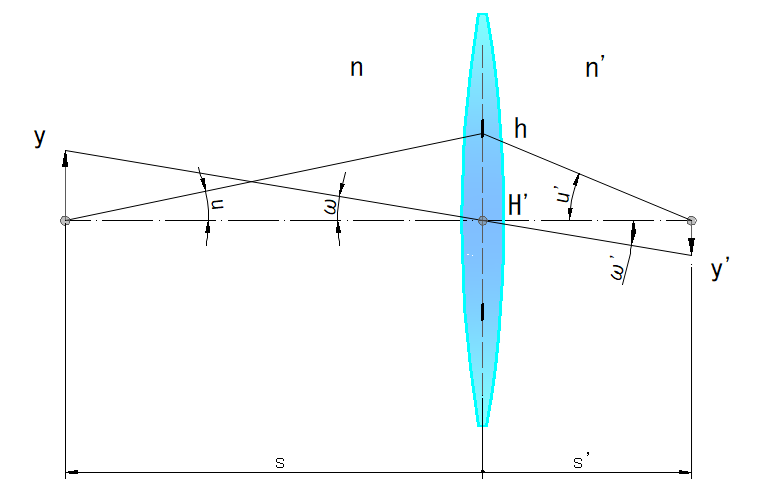
下記に前頁のラグランジュの不変量の式と正弦条件の式を、下図にラグランジュの不変量(左)と正弦条件(右)の概要図を示します
nuy = n’u’y’ ・・・ラグランジュの不変量
ny sin(u) = n’y’ sin(u’) ・・・正弦条件
両式において、u と sin(u) の違いがありますがほぼ同じ関係式です
ここで、ラグランジュの不変量において開口を大きくすると u の値と倍率が一致しません
これを補正するのが正弦条件と理解できます
正弦条件を算出する過程で、球面収差が補正される条件を前提とします
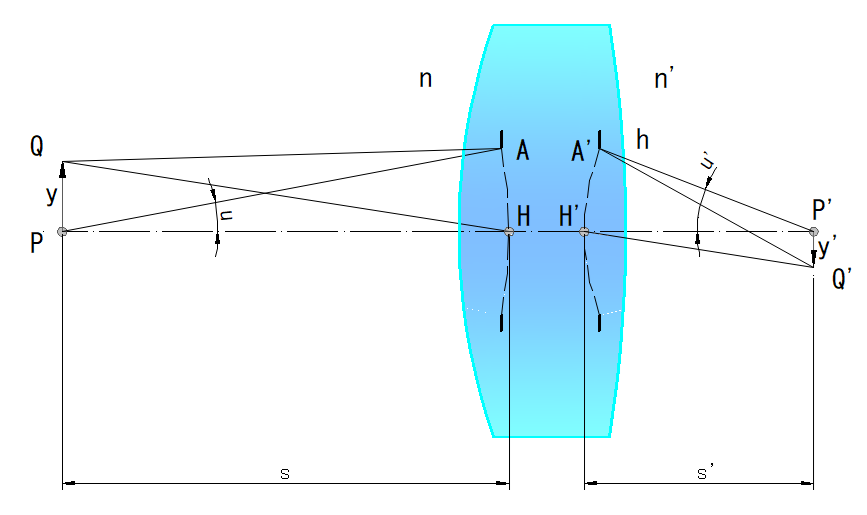
PH = PA, H’P’ = A’P’
これより、前側主面は物点Pを原点とする球面、像側主面は物点P’を原点とする球面になることが分かります
これは「物体からの球面波が収差無く像点に結像すること」と理解できます
入射側主面、射出側主面に適切な曲率を考えると、下右図において軸上物点⊿PAHと⊿QAHは(ほぼ)相似になります
従って、軸外物点のコマ収差が軽減できることになります
主面の形状とコマ収差
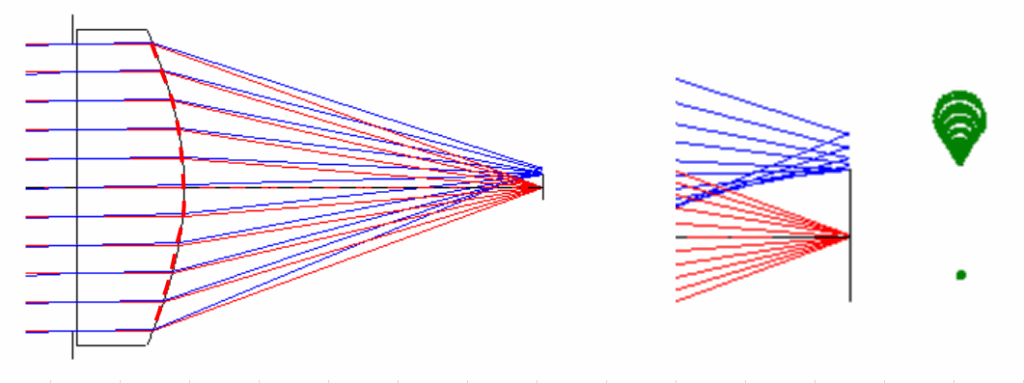
下図に平凸レンズを例にとり、収差の状態を示します(赤の点線_主面)
下左図は主面が後面になり、軸上光線と軸外光線の角度差が大きく正弦条件を逸脱しています
結果として、コマ収差が大きく発生します
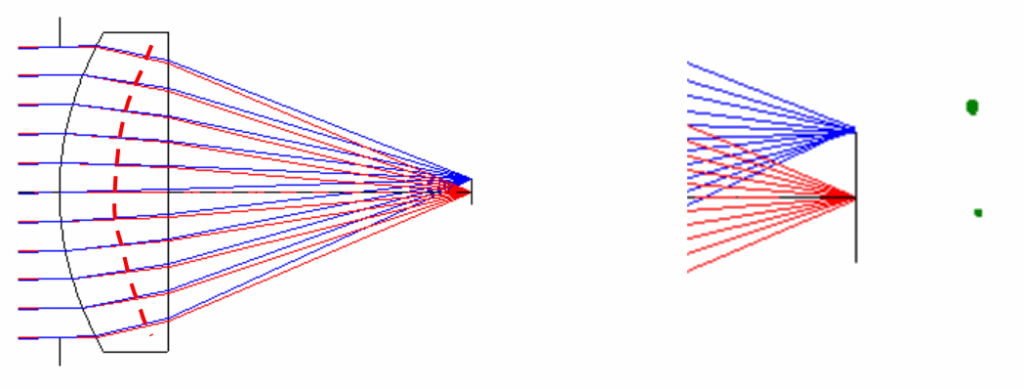
下右図は主面が像点を原点とする(ほぼ)球面です
この場合、コマ収差は低く抑えられます
このような事から正弦条件は主面の形状と考えることもできます