はじめに
収差は像のボヤけ、色のにじみ、歪などの総称です
収差を考える場合、単色収差と複色収差を分けて考える必要があります
ザイデル収差は単色収差で、正弦関数を級数展開した時の3次項までの近似に対し分類される収差です
・・・3次項までの近似式で表されるので、別に3次収差と言われます
sin(Θ) = Θ – Θ3/ 3!
ザイデル収差
・ 球面収差
・ コマ収差
・ 非点収差
・ 像面湾曲
・ 歪曲収差
球面収差(Spherical Aberration)
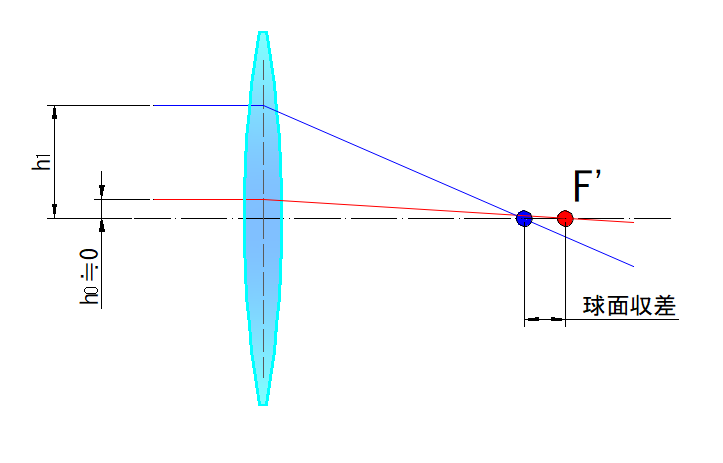
光軸に平行な光線を入射した時、焦点位置に光線が集まらない現象が球面収差です
下図において、光軸に限りなく近くを通過する光線(赤)に対し、光線高さ h1 の光線(青)は手前に集光しています
この集光点の位置の差が球面収差の量になります
球面収差の量は光線高さが高い(開口が大きい)ほど大きくなります
コマ収差(Comatic Aberration)
コマ収差は軸外物点からの光束が一点に集まらない収差です
彗星(Cimet)が尾を引く様子に似ていることが由来のようですが、諸説多々あります
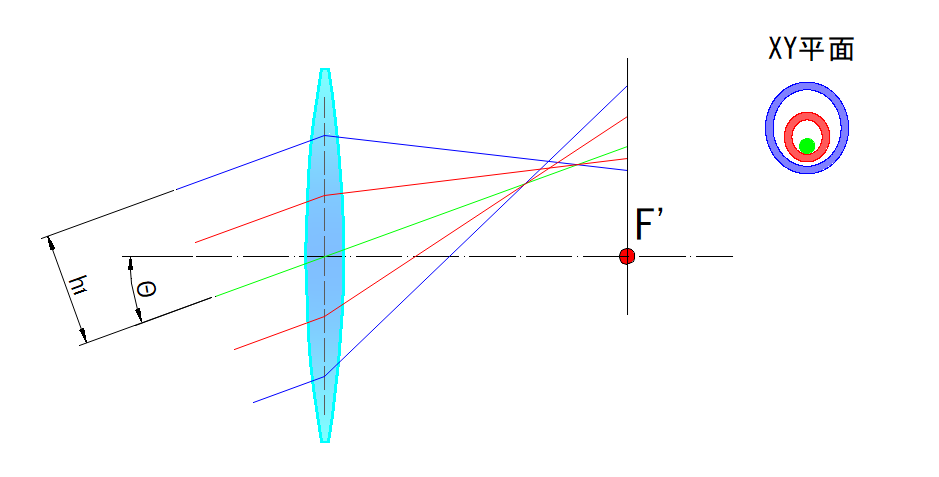
下図は平行光線が光軸とΘの角度を持って入射した状態で、その右側に瞳分割を円周上に取った像の状態を模擬的に示します
コマ収差は主光線に対して開口の開き径によって像位置がずれていく現象・・・光線高さ(h1)が高くなるに従ってコマ収差の量は増加
コマ収差は球面収差と似ているようですが、球面収差の無い光学系でも発生します
コマ収差を無くすには Abbe の正弦条件を満足する必要があります
※ 正弦条件_別途項を設けます
非点収差(Astigmatism)
非点収差は像位置での縦方向と横方向の焦点位置の差異(z方向)です
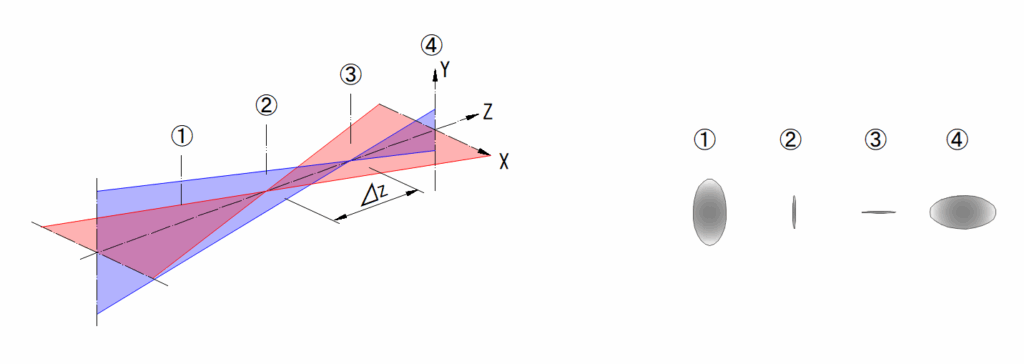
下左図は軸外物点がY軸と平行の位置で、その像位置でのメリジオナル平面とサジタル平面の集光状態です
縦方向の集光点(下図_②)と横方向の集光点(下図_③)との差異(⊿z)が非点収差です
一般的に、非点収差は像高さに応じ大きくなります
下右図は下左図のZ方向位置(①…④)での物体 点光源のスポットの状態
最良集光位置は②と③の中間になります
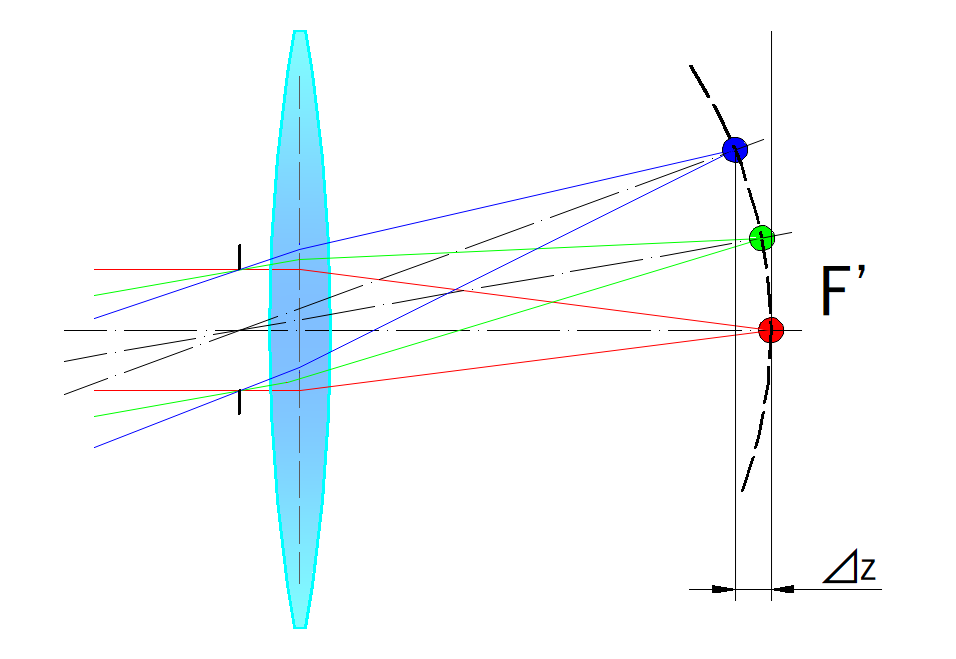
像面湾曲(Field Curvature)
像面湾曲は画角によって、像面が湾曲する収差です
下左図において、⊿zが像面湾曲の量です
像面湾曲を軽減するにはペッツバール和(Petzval Sum)を小さくします
例えばトリプレットレンズの場合、正レンズに屈折率の高い材料を使用し負レンズに屈折率の小さい材料を使用することで像面湾曲を低減できます
ペッツバール和
P _ペッツバール和
φn_レンズパワー
nn_レンズの屈折率
P = φ1/n1 + φ2/n2 + φ3/n3 + ・・・
歪曲収差(Distortion)
歪曲収差は前述の球面収差、コマ収差、非点収差、像面湾曲と異なり像品質に影響しない収差です
歪曲収差は理論的な像高さと実像高さの差異を理論的な像高さで割った値です
_理論的な像高さについてはピンホールカメラを思い浮かべてみて頂ければよいと思います
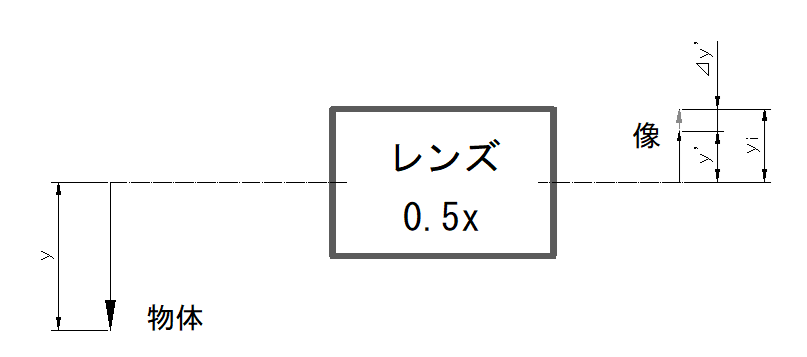
下図は高さ y の物体をレンズを通し倍率 0.5x で結像した概略図です
理想的な像高さ yi は
yi = y/2
これに対し実像高さ y’ と理想的な像高さ yi の差 ⊿y’を yi で割った値が歪曲収差(D) です
D = (yi – y’) / yi = ⊿y’ / yi
※ 歪曲収差の符号_理想像高さより実像高さが低ければ [-] 、高ければ [+]
[-]_ 樽型の歪曲収差 [+]_ 糸巻型の歪曲収差
※ ザイデル領域での歪曲収差は像高さの3乗で大きくなります