はじめに

前頁のザイデル収差は単一波長で発生する収差でした
レーザ光源などの単一波長の場合を除いて、一般的に多くのスペクトルを含む複色光です

光学材料は波長によって屈折率が異なります
従って単一レンズの場合波長によってレンズの焦点距離と、後側主点位置が異なることになり波長による像位がズレる収差が発生します

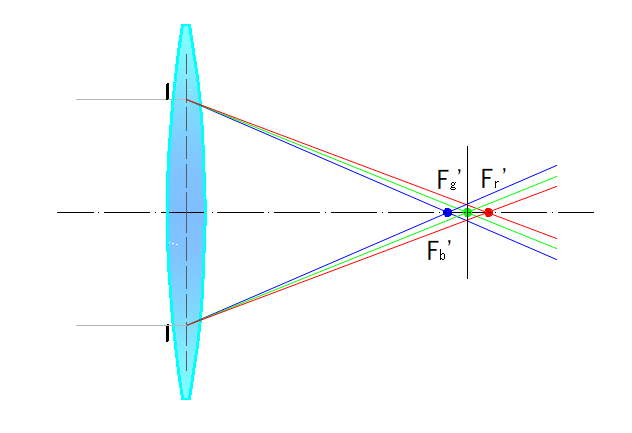
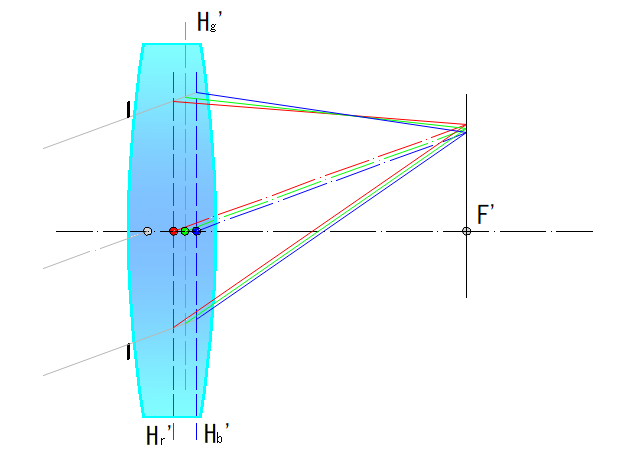
下左図に軸上色収差、下右図に倍率色収差の概要を示します

光学材料の主分散

光学材料のほとんどは波長に対し屈折率が変化します
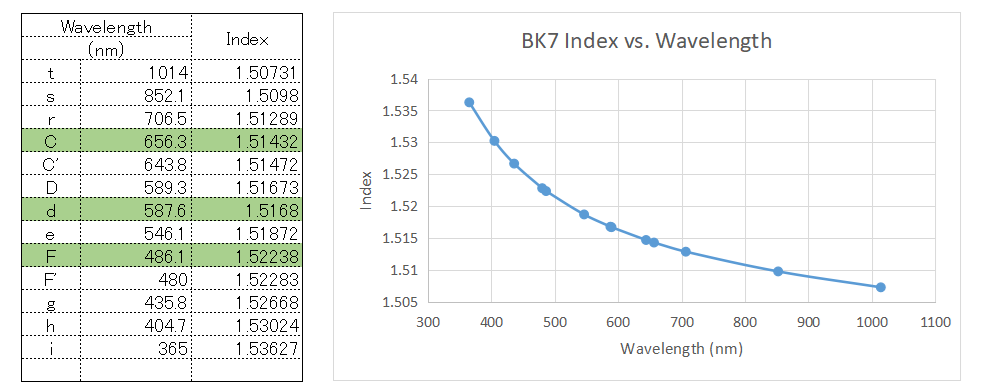
下図は代表的な光学ガラス材料 BK7 の波長に対する屈折率です

波長に対する屈折率の変化を分散と言い、特に明視野比視感度を基準にC線、Ｆ線を基準とした分散を主分散と言います
また光学材料の分散を主分散を用いて表した下記式をアッベ数（Abbe Number）と言います
このアッベ数は値が小さいほど分散が大きくなります

ν = (nd – 1) / (nF – nC)

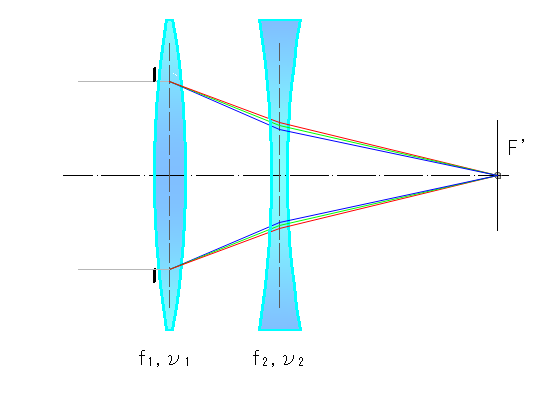
色消しの概要

単レンズでの色消しは不可能で、正レンズと負レンズの組み合わせで色消しを行います
下図は軸上色収差の色消しの概要です
正レンズで生じる各波長での焦点距離の変動を負レンズの逆向きの焦点距離の変動により補正します

一次の色消しの場合、下記の関係式が成り立ちます

f₁_ レンズ１の焦点距離　f₂_ レンズ１の焦点距離　f_ 全体の焦点距離
ν₁_ レンズ１のアッベ数　ν₂_ レンズ2のアッベ数

f₁ = (ν₁ -ν₂) / ν₁ ・f
f₂ = (ν₁ -ν₂) / ν₂ ・f